Théorie:
Afin de rendre constamment les roues artisanales de meilleure qualité, j’ai cherché à optimiser le transfert du couple de la roue arrière en étudiant de près la géométrie des roues.
La qualité du transfert du couple d’une roue dépend de deux angles que font les rayons en sortie du moyeu.
- Le premier angle est celui que fait le rayon quand on regarde la roue de côté, plus il est près de 90°, donc plus le rayon est tangentiel au moyeu, meilleur sera le transfert du couple. Si le rayon est parfaitement tangentiel au moyeu, on dira que le transfert du couple longitudinal ( CL ) est de 100%. Si le rayon est radial, on dira qu’il est nul puisque le rayon travaillera en flexion (et il n’est pas fait pour ça) plutôt qu’en traction.
- Le second angle est le parapluie de la roue. Quand on regarde la roue de derrière, il s’agit de l’angle entre le rayon et la droite imaginaire passant par le flasque du moyeu. Plus cet angle est près de 0°, meilleur sera le transfert du couple. Si cet angle s’approche de 90°, on dira que le transfert du couple transversal ( CT ) est nul (impossible d’avoir un angle de 90° ceci dit puisqu’il faudrait un moyeu de largeur infinie). Cette angle est toujours très faible notamment côté roue libre, on peut presque le considérer négligeable dans le transfert du couple. (Il s’agit aussi d’un angle qui qualifiera la rigidité de la roue.)
Le transfert du couple total de la roue sera alors caractérisé par ces deux pourcentages.

Pour connaître CL, il faut donc déterminer en premier l’angle caractérisant le transfert du couple longitudinal.
On connaît l’angle du parapluie et la longueur du rayon, on détermine donc sa projection sur la droite imaginaire crée par le flasque du moyeu:

On a donc:

A partir de cette longueur, on appliquera le théorème d’Al Kashi afin de déterminer l’angle caractérisant le transfert du couple longitudinal.
Recapitulatif du théorème d’Al-Kashi; on peut appliquer la formule du théorème de Pythagore généralisé à un triangle non rectangle;


A partir de la longueur B obtenue précedemment, on applique le théorème donc ce théorème dans le triangle suivant constitué par les droites A, B et C afin de déterminer l’angle vert. On recherche l’angle bleu qui est l’angle complémentaire à cet angle.
On obtient alors la formule pour TêtaL :
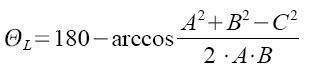
La valeur du cos-1 [A2+B2-C2/(2AB)] doit être multipliée par 57,296 dans le cas où vous seriez resté en radians. Cette valeur vient de 180/pi; le rapport entre les radians et les degrés.
On est à présent en mesure de déterminer CL la qualité du transfert de couple longitudinal par un produit en croix à partir de l’angle 90° et son transfert de 100%.
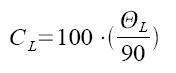
Dans le même ordre d’idée, on établit la courbe de la fonction de transfert du couple transversal en fonction de l’angle du parapluie, on obtient la relation suivante:

L= longueur du rayon
A= rayon du flasque du moyeu
B= projection de la longueur du rayon sur le plan imaginaire créé par le flasque du moyeu
C= Rayon effectif de la jante
ӨL= angle de transfert de couple dans le plan du flasque du moyeu
ӨT= angle de transfert de couple dans le plan transversal au flasque du moyeu (parapluie)
Exemple:
Exemple de la roue arrière présentée dernièrement sur Roues Artisanales (Zipp 285, TUNE Mag190, 28 rayons croisés à 3):
On a L= 273,3mm (théorique) et ӨT= 4.4° donc B= 272,5mm. On obtient alors ӨL = 80° et donc CL=88%. Aussi, on obtient par la dernière formule de l’article CT=95%.
On détermine donc la qualité du couple droit total par la dernière formule; CTotal = 84%.
Interprétation:
La qualité du couple total côté droit est de 84% ce qui signifie que si l’on applique un couple au moyeu, un rayon sur deux ( les rayons pousseurs n’agissent que lors des phases de freinage) transmettra 84% du couple par de la traction.
Les 16% restants seront donc transmis par de la flexion. Les rayons ne sont pas fait pour travailler en flexion puisqu’ils subissent des déformations qu’ils ne sont pas fait pour encaisser et il est donc évident qu’on va chercher à obtenir un ӨT et un ӨL le plus proche de 90 et 0° pour minimiser la fatigue des rayons.
Cependant, certaines roues comme les Neutron qui sont parmi les roues les plus solides et fiable du marché sont montées avec un rayonnage radial côté opposé roue libre. Ceci s’explique par le fait que le côté opposé roue libre transmet moins de couple que le côté roue libre (environ 85%/15%) , les rayons côté gauche subissent donc une flexion évaluée comme négligeable compte tenu de la qualité des rayons actuels. De plus, ces roues possèdent des écrous spécifiques afin de minimiser les contraintes au niveau de la tête du rayon.
Un autre contre exemple concerne les Ksyrium qui ont un rayonnage radial côté roue libre. Ce type de rayonnage est facilité entre autres grâce à des rayons aux caractéristiques extraordinaires (mais qui perdent en tension rapidement), à un moyeu très rigide qui permet de retransmettre le couple le mieux possible et à une jante qui optimise le placement des écrous afin que les rayons côté opposé roue libre ne travaillent presque uniquement en traction.
J’ai établi cet article à partir de mes connaissances, si vous rencontrez le moindre problème ou erreurs dans l’article, n’hésitez pas à m’en faire part.

