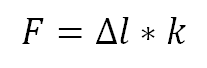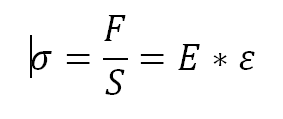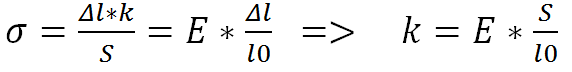Au tour des rayons d’être passés à la loupe ! Des rayons plus épais rendent-il la roue plus rigide ? Quel sont leurs avantages par rapport à des rayons plus fins ? Nous nous sommes amusés à les varier pour voir le résultat.
PROTOCOLE
Sur ce test, nous utiliserons toujours notre masse de 10kg, chargée perpendiculairement à la jante à un point précis comme sur les deux articles précédents sur les jantes asymétrique et symétrique et sur le comportement circulaire d’une roue à la déformation.
Les courbes suivantes indiquent la déformation de la roue sur sa circonférence, de 0° à 360° où la charge est appliquée. Les courbes sont en théorie symétriques en leur milieu.
Les mesures seront effectuées sur la zone plate de freinage car la déformation y est la plus importante : elle permet d’obtenir des résultats optimaux et représentatif de la réalité.
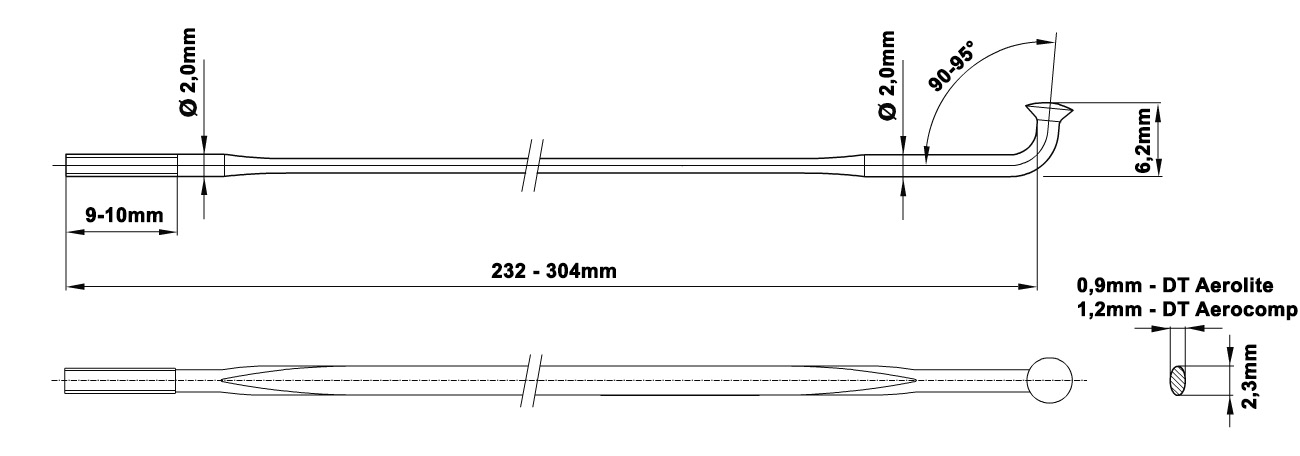
Ici, nous utilisons une seule roue, la RAR TEMPO 27 arrière à pneu, avec un moyeu DT Swiss 350, sur 24 rayons croisés par 2. Nous varions les rayons, des DT Swiss Aerolite 2,3/0.9 mm d’épaisseur ou des DT Swiss Aerocomp 2,3/1.2 mm d’épaisseur.
Les courbes affichées sont brutes, elles peuvent contenir des incertitudes de mesures. Les courbes en théorie symétrique peuvent ne pas l’être en pratique.
Déformations des roues sous une charge
Les tendances des courbes sont similaires entre les deux types de rayons, nous notons toutefois des différences dans les valeurs de déformations.
Sens de la charge: du côté cassette vers le côté opposé
Légende titre RL : Roue libre
|
Déformations aux points stratégiques |
|||
| Rayon n° | 1 (0/360°) | 13 (180°) | |
| Déformation Aerolite/Aerolite
(Courbe verte – référence) |
2.78 mm | -0.53 mm | |
| Déformation Aerocomp/Aerocomp
(Courbe rouge) |
-11% | -11% | |
| Déformation Aerolite/Aerocomp roue libre
(Courbe jaune) |
-6% | -3% | |
| Déformation Aerocomp/Aerolite roue libre
(Courbe noire) |
-8% | -15% | |
Sur ce graphique :
-
La courbe verte représentant la roue à rayons DT Swiss Aerolite des deux côtés est celle qui subit le plus de déformations sur toute sa circonférence. La déformation est la plus importante également au niveau des patins de freins. Il s’agit de la courbe de référence sur notre tableau.
-
La courbe rouge de la roue à rayons DT Swiss Aerocomp des deux côtés est celle qui subit le moins de déformations sur les 360°. Le comportement est en revanche identique car elle passe le seuil du zéro au même niveau que les autres, c’est à dire vers le 6ème (75°) et le 19ème (285°) rayons.
-
La courbe jaune de la roue à rayons DT Swiss Aerocomp côté roue libre et des rayons DT Swiss Aerolite côté opposé à la roue libre est située au milieu des deux courbes précédentes. Elle offre globalement une déformation à mi-chemin entre la rouge et la verte.
-
La courbe noire de la roue à rayons DT Swiss Aerolite côté roue libre et des rayons DT Swiss Aerocomp côté opposée à la roue libre est quasiment identique à la roue de la courbe jaune mais présente des déformations moins prononcées.
Première conclusion pour la roue RAR TEMPO testée à la déformation avec charge du côté cassette vers le côté opposé: les rayons Aerocomp offrent sans surprise un surplus de raideur qui se chiffre à environ 11% vis à vis de la roue de base. Lorsqu’ils sont rayonnés d’un côté ou l’autre de la roue, ces rayons de section supérieure ont une influence plus intéressante du côté opposé à la cassette, particulièrement dans la zone des 180° où l’on passe de -3% à -15% de déflexion, en tout cas dans ce sens de chargement.
Sens de la charge: du côté opposé vers le côté cassette
| Déformations aux points stratégiques | ||
| Rayon n° | 1 (0°/360°) | 13 (180°) |
| Déformation Aerolite/Aerolite
(Courbe verte – référence) |
2.87 mm | -0.60 |
| Déformation Aerocomp/Aerocomp
(Courbe rouge) |
-17% | -25% |
| Déformation Aerolite/Aerocomp roue libre
(Courbe jaune) |
-11% | -12% |
| Déformation Aerocomp/Aerolite roue libre
(Courbe noire) |
-12% | -21% |
Sur le graphique ci-dessus, le comportement et l’ordre des courbes est le même que sur le premier graphique de l’article. Les mêmes relevés et remarques peuvent être faîtes et les différences sont grandement amplifiées.
De nouvelles conclusions peuvent être tirées à partir de ces valeurs.
D’une part, nous constatons en effet que les surplus de raideur (en %) sur cette RAR TEMPO, sont supérieurs à ce que nous avions dans le tableau précédent. L’influence du rayon plus rigide est donc supérieure dans ce sens de déformation de la roue (côté opposé cassette vers côté cassette) que dans l’autre.
D’autre part, lorsqu’un seul côté de la roue est équipé des rayons de forte section, nous réalisons une nouvelle fois, comme sur le test précédent, qu’ils influent le plus sur la raideur de la roue quand ils sont placés côté opposé à la cassette. Signe que la distance flasque/centre de roue, révélatrice en partie de la tenue latérale de la roue, est plus bénéfique à des rayons épais que fins.
De cette seconde conclusion nous pouvons en extrapoler une 3ème: si ce rayon épais 2,3/1,2 a plus d’influence sur la raideur de la roue quand il est placé au plus loin du centre de la roue (le distance flasque opposé cassette/centre de roue est supérieure à la distance côté cassette/centre), c’est que cette distance flasque/centre de roue a une influence d’autant plus importante sur la tenue latérale de la roue.
Logique mais toujours bon de le vérifier. Si l’on vous pousse alors que vous avez les jambes espacées, vous resterez stable, si vos pieds sont rapprochés, vous perdrez votre stabilité. C’est pareil sur la roue. Nous nous pencherons plus en détail sur ces distances flasques/centre de roue dans un prochain article.
Quel rapport entre raideur rayon et raideur roue?
Suite à tous ces résultats nous pouvons faire des rapprochements concernant la rigidité du rayon vis à vis de la roue qu’il maintient. Lors de la déformation de la roue, la jante fléchit, le rayon suit donc la jante, il subit à la fois une flexion en plus du changement certain de sa tension originale (vérifié dans cet article).
– Vis à vis du changement de tension, un côté de la roue se détend, l’autre se retend, nous utiliserons alors la loi de Hooke pour approcher un changement dans la raideur.
– Concernant la flexion, nous la négligerons. En effet les valeurs de déformations latérales sur une roue étant de l’ordre de grandeur du millimètre, les valeurs de flèche du rayon sur la roue déformée sont donc extrêmement faibles.
La photo ci-dessous illustre ce phénomène de flèche sur le rayon DT Aerolite 2,3/0,9 qui se courbe bien plus que le DT Aerocomp 2,3/1,2. Tous deux de même longueur et ancrés de la même manière, le moment quadratique est imagé car très fortement amplifié par rapport à notre cas d’étude.
Le surplus de matière du Aerocomp par rapport à l’Aerolite peut être facilement calculé, et les résultats précédents nous donnent une information capitale pour établir l’influence de la rigidité rayon/rigidité roue.
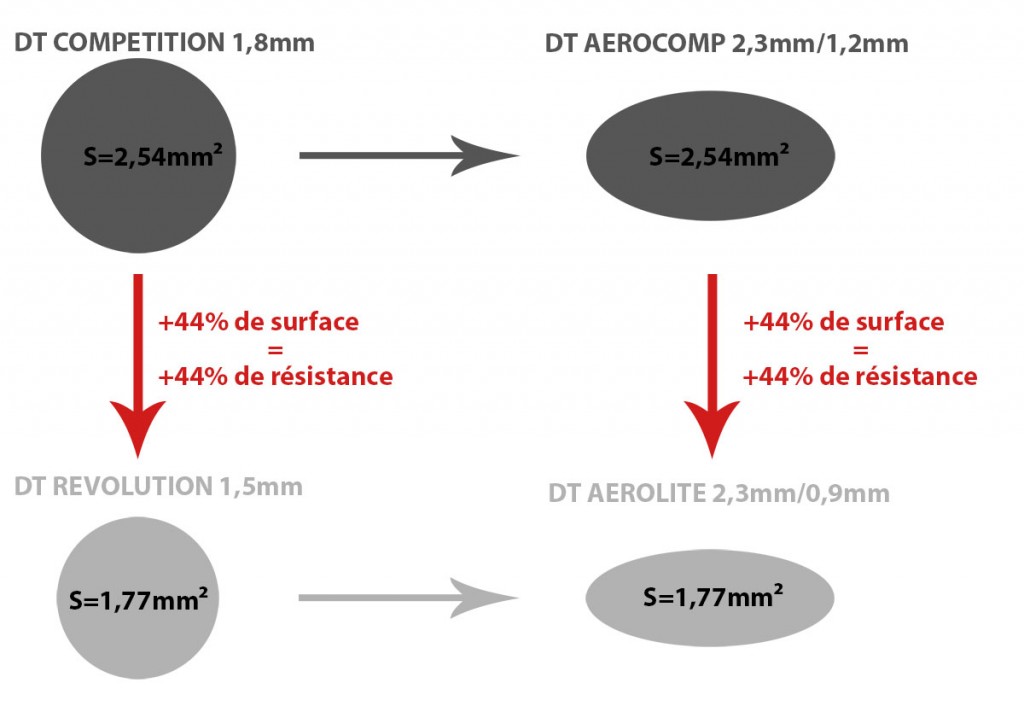
Les rayons Aerolite et Aerocomp sont les versions « aplaties » des rayons Revolution et Competition, la forme est différente mais la quantité de matière est identique, respectivement. Ce surplus de matière est directement lié à la différence de raideur à l’allongement.
Nous pouvons appliquer ici la loi de Hooke car nous avons soumis nos rayon a un effort de traction. Déjà étirés par leur tension mécanique, même sans déformation de roue, le chargement modifie la tension à la hausse ou à la baisse. Dans les cas extrêmes, les rayons perdant de la tension seront totalement détendus.
La loi de Hooke, ou plus précisément la loi des ressorts, définit la force appliquée au rayon qui est égale à sa variation de longueur, multipliée par sa raideur.
Afin de ne pas prendre en compte la forme de la pièce, Hooke a simplifié :
Avec ε=Δl/l0 la déformation et E le module d’élasticité longitudinal (module de young).
On obtient donc:
En l’occurrence dans cette formule, nous avons plusieurs paramètres identiques à savoir le matériau (E), la longueur initiale (l0) et une simplification sur la déformée de la roue.
Il est donc simple de faire le raccourci surplus de section = surplus résistance à la traction = surplus de rigidité roue.
Dans notre cas, la différence de section/quantité matière entre le DT Aerolite (DT Revolution) et DT Aerocomp (DT Competition) est de 44%: le DT Aerocomp dispose de 44% de matière en plus que le DT Aerolite. Il est donc 44% plus rigide à l’allongement ce qui se traduit en pratique, en moyenne, par +11% et +17% d’un côté puis l’autre de la roue.
Que conclure de tout cela ?
La section du rayon influe sur la quantité de matière résistante à l’allongement. Elle influe logiquement aussi sur sa masse à hauteur d’environ 60g sur une paire de roues (+1,3g en 296mm).
Ce gain de masse s’accompagne d’un surplus de raideur consécutif à la hausse de résistance à l’allongement et à la flexion du rayon. En arrondissant les valeurs enregistrées, à matériau égal, un rayon 50% plus résistant qu’un autre réalisera une roue environ 15% plus rigide.
Elargissement…
Lorsque la charge s’applique sur la jante, typique d’un coureur en danseuse, la roue se déforme, conséquence de la déflexion jante+rayon, selon la géométrie du rayon (étude dans un prochain article!). Ce mouvement ne suit pas simplement un axe latéral comme mis en valeur dans cet article, mais aussi l’axe vertical, très discrètement. En clair lors de la force latérale, la jante pivote autour du moyeu. Par curiosité nous avons vérifié ce phénomène avec une charge de 10kg latéral. La jante a subit une déflexion de 1,89mm latéralement, et aussi 0,08mm verticalement. Affaire à suivre…